The Schroedinger equation example..
This example depends on heat-equation.
Introduction
This example shows how to use the FFT and iFFT implementations in Ginkgo to solve the non-linear Schrödinger equation with a splitting method.
The non-linear Schrödinger equation (NLS) is given by
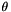
Here 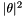 is the wave function of a single particle in two dimensions. Its magnitude
is the wave function of a single particle in two dimensions. Its magnitude 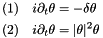 describes the probability distribution of the particle's position.
describes the probability distribution of the particle's position.
This equation can be split in to its linear (1) and non-linear (2) part
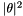
For both of these equations, we can compute exact solutions, assuming periodic boundary conditions and using the Fourier series expansion for (1) and using the fact that 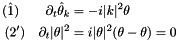 is constant in (2):
is constant in (2):
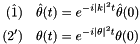
The exact solutions are then given by
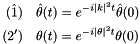
These partial solutions can be used to approximate a solution to the full NLS by alternating between small time steps for (1) and (2).
For nicer visual results, we add another constant potential term V(x) \theta to the non-linear part, which turns it into the Gross–Pitaevskii equation.
About the example
The commented program
\f}
The exact solutions are then given by
\f{align*}{
(\hat 1) \quad \hat\theta(t) &= e^{-i |k|^2 t} \hat\theta(0)\\
(2') \quad \theta(t) &= e^{-i |\theta|^2 t} \theta(0)
\f}
These partial solutions can be used to approximate a solution to the full NLS
by alternating between small time steps for (1) and (2).
For nicer visual results, we add another constant potential term V(x) \theta
to the non-linear part, which turns it into the Gross–Pitaevskii equation.
*****************************<DESCRIPTION>********************************** /
#include <algorithm>
#include <chrono>
#include <fstream>
#include <iostream>
#include <utility>
#include <opencv2/core.hpp>
#include <opencv2/videoio.hpp>
#include <ginkgo/ginkgo.hpp>
This function implements a simple Ginkgo-themed clamped color mapping for values in the range [0,5].
void set_val(unsigned char* data, double value)
{
RGB values for the 6 colors used for values 0, 1, ..., 5 We will interpolate linearly between these values.
double col_r[] = {255, 221, 129, 201, 249, 255};
double col_g[] = {255, 220, 130, 161, 158, 204};
double col_b[] = {255, 220, 133, 93, 24, 8};
value = std::max(0.0, value);
auto i = std::max(0, std::min(4, int(value)));
auto d = std::max(0.0, std::min(1.0, value - i));
OpenCV uses BGR instead of RGB by default, revert indices
data[2] = static_cast<unsigned char>(col_r[i + 1] * d + col_r[i] * (1 - d));
data[1] = static_cast<unsigned char>(col_g[i + 1] * d + col_g[i] * (1 - d));
data[0] = static_cast<unsigned char>(col_b[i + 1] * d + col_b[i] * (1 - d));
}
Initialize video output with given dimension and FPS (frames per seconds)
std::pair<cv::VideoWriter, cv::Mat> build_output(int n, double fps)
{
cv::Size videosize{n, n};
auto output =
std::make_pair(cv::VideoWriter{}, cv::Mat{videosize, CV_8UC3});
auto fourcc = cv::VideoWriter::fourcc('a', 'v', 'c', '1');
output.first.open("nls.mp4", fourcc, fps, videosize);
return output;
}
Write the current frame to video output using the above color mapping
void output_timestep(std::pair<cv::VideoWriter, cv::Mat>& output, int n,
const std::complex<double>* data)
{
for (int i = 0; i < n; i++) {
auto row = output.second.ptr(i);
for (int j = 0; j < n; j++) {
set_val(&row[3 * j],
abs(data[i * n + j]));
}
}
output.first.write(output.second);
}
int main(int argc, char* argv[])
{
Problem parameters: simulation length
scaling factor for non-linearity
const auto nonlinear_scale = 1.0;
scaling factor for potential
const auto potential_scale = 3.0;
Simulation parameters: time scaling factor
const auto time_scale = 0.25;
number of grid points in each dimension
number of simulation steps per second
const auto steps_per_sec = 1000;
number of video frames per second
number of grid points
phase difference between neighboring grid points
const auto h = 2.0 * gko::pi<double>() / n;
const auto h2 = h * h;
time step size for the simulation
const auto tau = 1.0 / steps_per_sec;
const auto idx = [&](int i, int j) { return i * n + j; };
create an OpenMP executor
load initial state vector
std::ifstream initial_stream("data/gko_logo_2d.mtx");
std::ifstream potential_stream("data/gko_text_2d.mtx");
auto amplitude = gko::read<vec>(initial_stream, exec);
auto potential = gko::read<real_vec>(potential_stream, exec);
create vector for frequency space representation
auto frequency = vec::create(exec, amplitude->get_size());
create Fourier matrix
auto fft = fft2::create(exec, n, n);
auto ifft = fft->conj_transpose();
prepare video output
auto output = build_output(n, fps);
time stamp of the last output frame (sentinel value)
execute splitting method: time step in linear part, then non-linear part
for (double t = 0; t < t0; t += tau) {
if enough time has passed, output the next frame
if (t - last_t > 1.0 / fps) {
last_t = t;
std::cout << t << std::endl;
output_timestep(output, n, amplitude->get_const_values());
}
time step in linear part
fft->apply(amplitude, frequency);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
frequency->at(idx(i, j)) *=
std::polar(1.0, -h2 * (i * i + j * j) * tau * time_scale);
scale by FFT*iFFT normalization factor
frequency->at(idx(i, j)) *= 1.0 / n2;
}
}
ifft->apply(frequency, amplitude);
time step in non-linear part
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
amplitude->at(idx(i, j)) *= std::polar(
1.0, -(nonlinear_scale *
potential_scale * potential->at(idx(i, j))) *
tau * time_scale);
}
}
}
}
Results
The program will generate a video file named nls.mp4 and output the timestamp of each generated frame.
Comments about programming and debugging
The plain program
#include <algorithm>
#include <chrono>
#include <fstream>
#include <iostream>
#include <utility>
#include <opencv2/core.hpp>
#include <opencv2/videoio.hpp>
#include <ginkgo/ginkgo.hpp>
void set_val(unsigned char* data, double value)
{
double col_r[] = {255, 221, 129, 201, 249, 255};
double col_g[] = {255, 220, 130, 161, 158, 204};
double col_b[] = {255, 220, 133, 93, 24, 8};
value = std::max(0.0, value);
auto i = std::max(0, std::min(4, int(value)));
auto d = std::max(0.0, std::min(1.0, value - i));
data[2] = static_cast<unsigned char>(col_r[i + 1] * d + col_r[i] * (1 - d));
data[1] = static_cast<unsigned char>(col_g[i + 1] * d + col_g[i] * (1 - d));
data[0] = static_cast<unsigned char>(col_b[i + 1] * d + col_b[i] * (1 - d));
}
std::pair<cv::VideoWriter, cv::Mat> build_output(int n, double fps)
{
cv::Size videosize{n, n};
auto output =
std::make_pair(cv::VideoWriter{}, cv::Mat{videosize, CV_8UC3});
auto fourcc = cv::VideoWriter::fourcc('a', 'v', 'c', '1');
output.first.open("nls.mp4", fourcc, fps, videosize);
return output;
}
void output_timestep(std::pair<cv::VideoWriter, cv::Mat>& output, int n,
const std::complex<double>* data)
{
for (int i = 0; i < n; i++) {
auto row = output.second.ptr(i);
for (int j = 0; j < n; j++) {
set_val(&row[3 * j],
abs(data[i * n + j]));
}
}
output.first.write(output.second);
}
int main(int argc, char* argv[])
{
const auto t0 = 15.0;
const auto nonlinear_scale = 1.0;
const auto potential_scale = 3.0;
const auto time_scale = 0.25;
const auto n = 256;
const auto steps_per_sec = 1000;
const auto fps = 25;
const auto n2 = n * n;
const auto h = 2.0 * gko::pi<double>() / n;
const auto h2 = h * h;
const auto tau = 1.0 / steps_per_sec;
const auto idx = [&](int i, int j) { return i * n + j; };
std::ifstream initial_stream("data/gko_logo_2d.mtx");
std::ifstream potential_stream("data/gko_text_2d.mtx");
auto amplitude = gko::read<vec>(initial_stream, exec);
auto potential = gko::read<real_vec>(potential_stream, exec);
auto frequency = vec::create(exec, amplitude->get_size());
auto fft = fft2::create(exec, n, n);
auto ifft = fft->conj_transpose();
auto output = build_output(n, fps);
double last_t = -t0;
for (double t = 0; t < t0; t += tau) {
if (t - last_t > 1.0 / fps) {
last_t = t;
std::cout << t << std::endl;
output_timestep(output, n, amplitude->get_const_values());
}
fft->apply(amplitude, frequency);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
frequency->at(idx(i, j)) *=
std::polar(1.0, -h2 * (i * i + j * j) * tau * time_scale);
frequency->at(idx(i, j)) *= 1.0 / n2;
}
}
ifft->apply(frequency, amplitude);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
amplitude->at(idx(i, j)) *= std::polar(
1.0, -(nonlinear_scale *
potential_scale * potential->at(idx(i, j))) *
tau * time_scale);
}
}
}
}


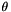
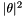 is the wave function of a single particle in two dimensions. Its magnitude
is the wave function of a single particle in two dimensions. Its magnitude 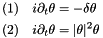 describes the probability distribution of the particle's position.
describes the probability distribution of the particle's position.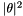
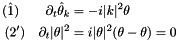 is constant in (2):
is constant in (2):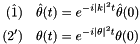
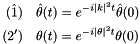
 1.8.16
1.8.16