Adding Unified Kernels

Ginkgo provides a unified kernel framework to facilitate adding new kernels to all of the non-Reference backends with one kernel definition. These unified kernels are defined in common/unified/. The key to these kernels is the run_kernel_ functions defined by Ginkgo. Each unified kernel can launch one or more device/OpenMP kernels through the run_kernel_ options.

There are three main types of run_kernel_ routines in Ginkgo: standard, solver, and reduction.

Standard kernels

Ginkgo has two types of standard unified kernels: 1D and 2D. The size parameter determines which kind of kernel is launched, with a single size_type value launching a 1D kernel, while a gko::dim<2> parameter will launch a 2D kernel.

The interface for calling a standard unified kernel within a Ginkgo kernel is

 run_kernel(std::shared_ptr<Executor> exec, // Executor
            KernelFunction fn, // lambda function defining kernel
            [size_type or dim<2>] size,
            KernelArgs&&... args // parameters passed on to the lambda function 
 );

For a 1D kernel, the first parameter of fn must be a flat index i. For the GPU backends, this is the thread ID as defined by thread::get_thread_id_flat. This index is not included in args in the call to run_kernel. So, for example, consider the simple 1D scale kernel (part of common/unified/matrix/csr_kernels.cpp). Its lambda function is

[] GKO_KERNEL(auto nnz, auto alpha, auto x) { x[nnz] *= alpha[0]; }

where nnz is the index variable, and alpha is the scaling factor for x. Each thread scales its entry in x by alpha. The full kernel launch code is

 run_kernel(
        exec,
        [] GKO_KERNEL(auto nnz, auto alpha, auto x) { x[nnz] *= alpha[0]; },
        x->get_num_stored_elements(), // size
        alpha->get_const_values(), // alpha -- first non-index arg of the lambda function
        x->get_values()); // x -- second non-index arg

For a 2D kernel, the first two parameters taken by fn must correspond to row and col. For the OpenMP backend, the lambda function will be called inside loops: an outer loop on rows, which is parallelized with #pragma omp parallel, and explicitly unrolled inner loop(s) for col. For the GPU backends, row and col are determined by

row = tidx / cols;
col = tidx % cols;

with tidx the flat thread ID. As with the 1D kernel, these two parameters are not included in the parameters passed in args, since they are part of Ginkgo’s kernel launch infrastructure.

Solver kernels

Solver kernels are like standard 2D kernels, but with additional support to handle the many Dense objects that may be passed as arguments. Often, many of the Dense parameters will either have the same stride, or have a stride of 1 (and thus be able to be treated directly as a plain array of data). Ginkgo’s solver kernel framework allows us to take advantage of this fact and simplify the definition of the kernel launch, without needing to pass a stride parameter for every Dense argument.

The interface for calling a solver kernel looks like

 run_kernel_solver(std::shared_ptr<Executor> exec,
                   KernelFunction fn, // lambda function defining kernel
                   dim<2> size,
                   size_type default_stride, // default stride for Dense args 
                   KernelArgs&&... args // parameters passed on to the lambda function
 );

The solver kernels work like 2D standard kernels, in that the first two parameters of the lambda function must be row and col, which are handled the same way as in the standard kernel version. The main difference for solver kernels is the addition of the default_stride parameter and the use of helper functions in the args list. These helper functions can be seen in common/unified/base/kernel_launch_solver.hpp.

For the purposes of using the unified solver kernel framework, it’s enough to know that we can mark Dense kernel arguments as having either stride 1 (a row_vector) or default_stride. For example, consider the step_2 kernel in the CG solver, which updates the solution (x) and residual (r) vectors:

 run_kernel_solver(
        exec,
        [] GKO_KERNEL(auto row, auto col, auto x, auto r, auto p, auto q,        
                      auto beta, auto rho, auto stop) {                          
            if (!stop[col].has_stopped()) {
                auto tmp = safe_divide(rho[col], beta[col]);                     
                x(row, col) += tmp * p(row, col);                                
                r(row, col) -= tmp * q(row, col);                                
            }                                                                    
        },                                                                       
        x->get_size(), // size for 2D kernel launch
        r->get_stride(), // default stride
        x, // first non-index arg
        default_stride(r), default_stride(p), default_stride(q),
        row_vector(beta), row_vector(rho), *stop_status);    

Note that of the Dense arguments, r, p, and q are marked as having the default stride, which is the stride of r, while beta and rho have stride 1 (beta and rho are scalar values for each right hand side being solved). x does not have a stride marked because it is the solution vector. Unlike the other Dense arguments, is passed to the solver by the user, rather than created by the solver. x could have a different stride than its number of columns if, for example, it is actually a submatrix of a larger matrix.

Reduction kernels

The final kind of unified kernel in Ginkgo is the reduction kernel. These kernels perform a computation, then do a reduction operation on the resulting temporary values computed by each thread.

Reduction kernels come in 4 flavors: 1D, 2D, row, and column. Their interfaces are a little more complicated than the standard or solver kernels:

/* 1D or 2D reduction kernel -- reduce to single value */
  
 run_kernel_reduction(std::shared_ptr<Executor> exec,
                      KernelFunction fn, // main lambda function defining kernel
                      ReductionOp op, // lambda function for reduction operation
                      FinalizeOp finalize, // lambda function for finalization
                      ValueType identity, // the identity operator
                      ValueType* result, // pointer to location for result
                      [size_type or dim<2>] size,
                      KernelArgs&&... args)

/* Row reduction kernel -- reduce across rows, produce a column */

 run_kernel_row_reduction(std::shared_ptr<Executor> exec,
                          KernelFunction fn, // main lambda function defining kernel
                          ReductionOp op, // lambda function for reduction operation
                          FinalizeOp finalize, // lambda function for finalization
                          ValueType identity, // the identity operator
                          ValueType* result, // pointer to location for result
                          size_type result_stride, // stride for result column 
                          dim<2> size, // size must be 2D
                          KernelArgs&&... args)

/* Column reduction kernel -- reduce across columns, produce a row */
 
 run_kernel_col_reduction(std::shared_ptr<Executor> exec,
                          KernelFunction fn, // main lambda function defining kernel
                          ReductionOp op, // lambda function for reduction operation
                          FinalizeOp finalize, // lambda function for finalization
                          ValueType identity, // the identity operator
                          ValueType* result, // pointer to location for result
                          dim<2> size, // size must be 2D
                          KernelArgs&&... args)

In Figure 1 we give a visual representation of the four types of reduction kernels.

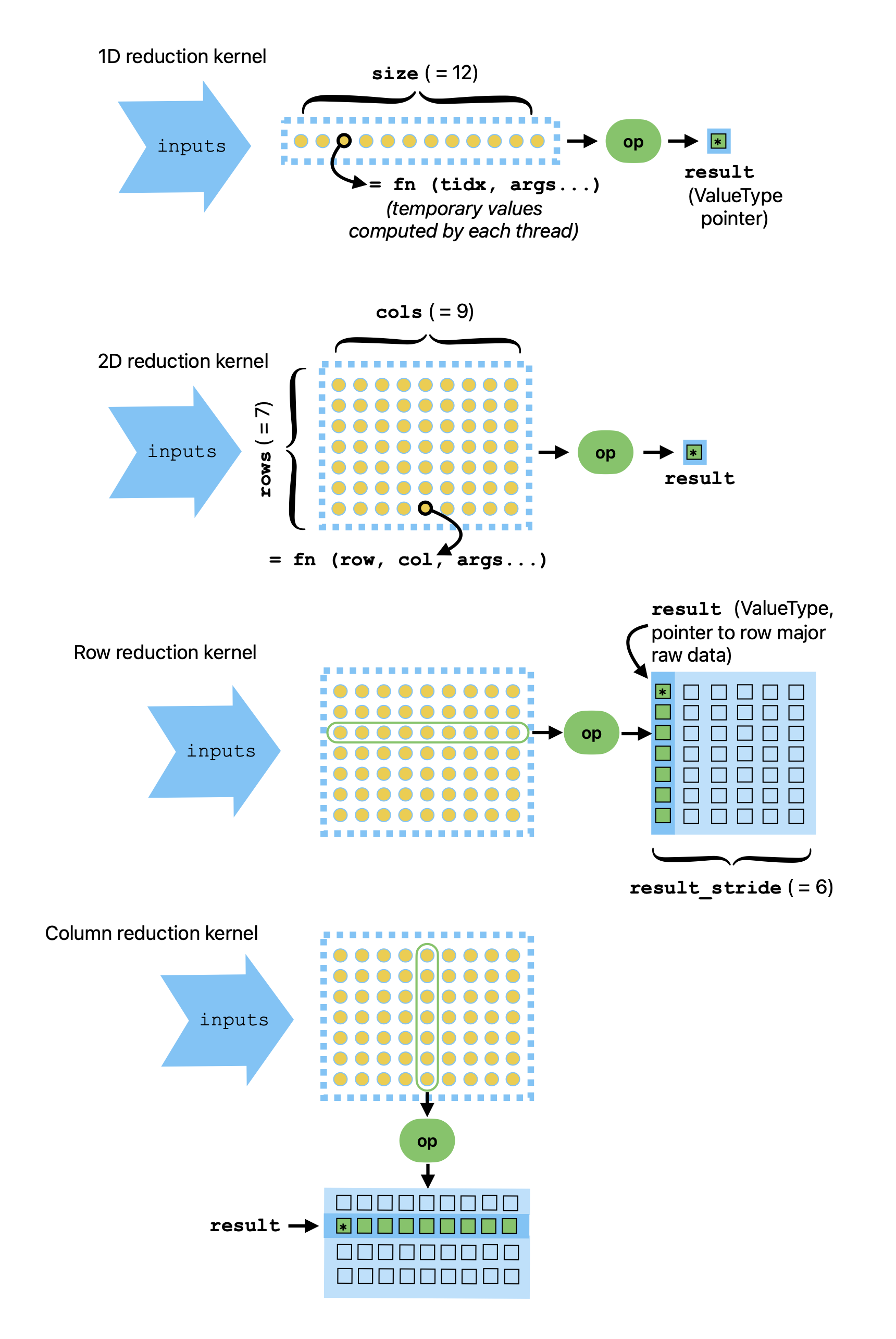
Using the four types of unified reduction kernels in Ginkgo.

As seen in the interfaces, all reduction kernels use three lambda functions rather than one. There is still a main KernelFunction defining the kernel; this specifies the computation done by each thread prior to the reduction. The reduction operation is also defined via lambda function. The finalize function can be used to perform one final operation prior to storing the result.

Ginkgo provides helpful macros for two common reduction cases: GKO_KERNEL_REDUCE_SUM and GKO_KERNEL_REDUCE_MAX. These macros expand to define the reduction operation, finalization operation, and identity operator for the kernel; in other words, the op, finalize, and identity parameters are replaced with a single macro when you call run_kernel_[row/col_]reduction. The usage then looks like the count_nonzeros_per_row kernel for a Dense matrix:

 run_kernel_row_reduction(
     exec,
     [] GKO_KERNEL(auto i, auto j, auto mtx) {
         return is_nonzero(mtx(i, j)) ? 1 : 0;
     },
     GKO_KERNEL_REDUCE_SUM(IndexType), // use macro to indicate a standard summation reduction
     result, // start of result column in memory
     1, // stride of result
     mtx->get_size(), // 2D size for kernel
     mtx // first (and only) non-index arg for fn
 );