A LinOpFactory represents a higher order mapping which transforms one linear operator into another. More...

#include <ginkgo/core/base/lin_op.hpp>

Inheritance diagram for gko::LinOpFactory:

Collaboration diagram for gko::LinOpFactory:

Public Member Functions
std::unique_ptr< LinOp >	generate (std::shared_ptr< const LinOp > input) const

Public Member Functions inherited from gko::PolymorphicObject
PolymorphicObject &	operator= (const PolymorphicObject &)

std::unique_ptr< PolymorphicObject >	create_default (std::shared_ptr< const Executor > exec) const
	Creates a new "default" object of the same dynamic type as this object. More...

std::unique_ptr< PolymorphicObject >	create_default () const
	Creates a new "default" object of the same dynamic type as this object. More...

std::unique_ptr< PolymorphicObject >	clone (std::shared_ptr< const Executor > exec) const
	Creates a clone of the object. More...

std::unique_ptr< PolymorphicObject >	clone () const
	Creates a clone of the object. More...

PolymorphicObject *	copy_from (const PolymorphicObject *other)
	Copies another object into this object. More...

template<typename Derived , typename Deleter >
std::enable_if_t< std::is_base_of< PolymorphicObject, std::decay_t< Derived > >::value, PolymorphicObject > *	copy_from (std::unique_ptr< Derived, Deleter > &&other)
	Moves another object into this object. More...

template<typename Derived , typename Deleter >
std::enable_if_t< std::is_base_of< PolymorphicObject, std::decay_t< Derived > >::value, PolymorphicObject > *	copy_from (const std::unique_ptr< Derived, Deleter > &other)
	Copies another object into this object. More...

PolymorphicObject *	copy_from (const std::shared_ptr< const PolymorphicObject > &other)
	Copies another object into this object. More...

PolymorphicObject *	move_from (ptr_param< PolymorphicObject > other)
	Moves another object into this object. More...

PolymorphicObject *	clear ()
	Transforms the object into its default state. More...

std::shared_ptr< const Executor >	get_executor () const noexcept
	Returns the Executor of the object. More...

Public Member Functions inherited from gko::log::EnableLogging< PolymorphicObject >
void	add_logger (std::shared_ptr< const Logger > logger) override

void	remove_logger (const Logger *logger) override

void	remove_logger (ptr_param< const Logger > logger)

const std::vector< std::shared_ptr< const Logger > > &	get_loggers () const override

void	clear_loggers () override

Public Member Functions inherited from gko::log::Loggable
void	remove_logger (ptr_param< const Logger > logger)

Detailed Description

A LinOpFactory represents a higher order mapping which transforms one linear operator into another.

In Ginkgo, every linear solver is viewed as a mapping. For example, given an s.p.d linear system 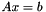$Ax = b$ , the solution $x = A^{-1}b$ can be computed using the CG method. This algorithm can be represented in terms of linear operators and mappings between them as follows:

A Cg::Factory is a higher order mapping which, given an input operator , returns a new linear operator $A^{-1}$ stored in "CG format"
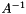Storing the operator $A^{-1}$ in "CG format" means that the data structure used to store the operator is just a simple pointer to the original matrix 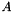. The application $x = A^{-1}b$ of such an operator can then be implemented by solving the linear system 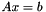using the CG method. This is achieved in code by having a special class for each of those "formats" (e.g. the "Cg" class defines such a format for the CG solver).

Another example of a LinOpFactory is a preconditioner. A preconditioner for a linear operator 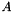$A$ is a linear operator 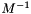$M^{-1}$ , which approximates 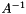$A^{-1}$ . In addition, it is stored in a way such that both the data of 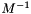$M^{-1}$ is cheap to compute from 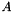$A$ , and the operation 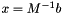$x = M^{-1}b$ can be computed quickly. These operators are useful to accelerate the convergence of Krylov solvers. Thus, a preconditioner also fits into the LinOpFactory framework:

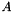The factory maps a linear operator into a preconditioner 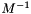$M^{-1}$ which is stored in suitable format (e.g. as a product of two factors in case of ILU preconditioners).
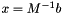The resulting linear operator implements the application operation $x = M^{-1}b$ depending on the format the preconditioner is stored in (e.g. as two triangular solves in case of ILU)

Example: using CG in Ginkgo

 {c++}
// Suppose A is a matrix, b a rhs vector, and x an initial guess
// Create a CG which runs for at most 1000 iterations, and stops after
// reducing the residual norm by 6 orders of magnitude
auto cg_factory = solver::Cg<>::build()
    .with_max_iters(1000)
    .with_rel_residual_goal(1e-6)
    .on(cuda);
// create a linear operator which represents the solver
auto cg = cg_factory->generate(A);
// solve the system
cg->apply(b, x);

The documentation for this class was generated from the following file:

ginkgo/core/base/lin_op.hpp

Public Member Functions

Detailed Description

Example: using CG in Ginkgo