A module dedicated to the implementation and usage of the Linear operators in Ginkgo. More...

Collaboration diagram for Linear Operators:

Modules
	SpMV employing different Matrix formats
	A module dedicated to the implementation and usage of the various Matrix Formats in Ginkgo.

	Preconditioners
	A module dedicated to the implementation and usage of the Preconditioners in Ginkgo.

	Solvers
	A module dedicated to the implementation and usage of the Solvers in Ginkgo.

Classes
class	gko::Combination< ValueType >
	The Combination class can be used to construct a linear combination of multiple linear operators `c1 * op1 + c2 * op2 + ... More...

class	gko::Composition< ValueType >
	The Composition class can be used to compose linear operators `op1, op2, ..., opn` and obtain the operator `op1 * op2 * ... More...

class	gko::LinOpFactory
	A LinOpFactory represents a higher order mapping which transforms one linear operator into another. More...

class	gko::ReadableFromMatrixData< ValueType, IndexType >
	A LinOp implementing this interface can read its data from a matrix_data structure. More...

class	gko::WritableToMatrixData< ValueType, IndexType >
	A LinOp implementing this interface can write its data to a matrix_data structure. More...

class	gko::Preconditionable
	A LinOp implementing this interface can be preconditioned. More...

class	gko::EnableLinOp< ConcreteLinOp, PolymorphicBase >
	The EnableLinOp mixin can be used to provide sensible default implementations of the majority of the LinOp and PolymorphicObject interface. More...

class	gko::matrix::Coo< ValueType, IndexType >
	COO stores a matrix in the coordinate matrix format. More...

class	gko::matrix::Csr< ValueType, IndexType >
	CSR is a matrix format which stores only the nonzero coefficients by compressing each row of the matrix (compressed sparse row format). More...

class	gko::matrix::Dense< ValueType >
	Dense is a matrix format which explicitly stores all values of the matrix. More...

class	gko::matrix::Ell< ValueType, IndexType >
	ELL is a matrix format where stride with explicit zeros is used such that all rows have the same number of stored elements. More...

class	gko::matrix::Hybrid< ValueType, IndexType >
	HYBRID is a matrix format which splits the matrix into ELLPACK and COO format. More...

class	gko::matrix::Identity< ValueType >
	This class is a utility which efficiently implements the identity matrix (a linear operator which maps each vector to itself). More...

class	gko::matrix::IdentityFactory< ValueType >
	This factory is a utility which can be used to generate Identity operators. More...

class	gko::matrix::Sellp< ValueType, IndexType >
	SELL-P is a matrix format similar to ELL format. More...

struct	gko::preconditioner::block_interleaved_storage_scheme< IndexType >
	Defines the parameters of the interleaved block storage scheme used by block-Jacobi blocks. More...

class	gko::preconditioner::Jacobi< ValueType, IndexType >
	A block-Jacobi preconditioner is a block-diagonal linear operator, obtained by inverting the diagonal blocks of the source operator. More...

class	gko::solver::Bicgstab< ValueType >
	BiCGSTAB or the Bi-Conjugate Gradient-Stabilized is a Krylov subspace solver. More...

class	gko::solver::Cg< ValueType >
	CG or the conjugate gradient method is an iterative type Krylov subspace method which is suitable for symmetric positive definite methods. More...

class	gko::solver::Cgs< ValueType >
	CGS or the conjugate gradient square method is an iterative type Krylov subspace method which is suitable for general systems. More...

class	gko::solver::Fcg< ValueType >
	FCG or the flexible conjugate gradient method is an iterative type Krylov subspace method which is suitable for symmetric positive definite methods. More...

class	gko::solver::Gmres< ValueType >
	GMRES or the generalized minimal residual method is an iterative type Krylov subspace method which is suitable for nonsymmetric linear systems. More...

Macros
#define	GKO_CREATE_FACTORY_PARAMETERS(_parameters_name, _factory_name)
	This Macro will generate a new type containing the parameters for the factory `_factory_name`. More...

#define	GKO_ENABLE_LIN_OP_FACTORY(_lin_op, _parameters_name, _factory_name)
	This macro will generate a default implementation of a LinOpFactory for the LinOp subclass it is defined in. More...

#define	GKO_ENABLE_BUILD_METHOD(_factory_name)
	Defines a build method for the factory, simplifying its construction by removing the repetitive typing of factory's name. More...

#define	GKO_FACTORY_PARAMETER(_name, ...)
	Creates a factory parameter in the factory parameters structure. More...

Typedefs
template<typename ConcreteFactory , typename ConcreteLinOp , typename ParametersType , typename PolymorphicBase = LinOpFactory>
using	gko::EnableDefaultLinOpFactory = EnableDefaultFactory< ConcreteFactory, ConcreteLinOp, ParametersType, PolymorphicBase >
	This is an alias for the EnableDefaultFactory mixin, which correctly sets the template parameters to enable a subclass of LinOpFactory. More...

Detailed Description

A module dedicated to the implementation and usage of the Linear operators in Ginkgo.

Below we elaborate on one of the most important concepts of Ginkgo, the linear operator. The linear operator (LinOp) is a base class for all linear algebra objects in Ginkgo. The main benefit of having a single base class for the entire collection of linear algebra objects (as opposed to having separate hierarchies for matrices, solvers and preconditioners) is the generality it provides.

Advantages of this approach and usage

A common interface often allows for writing more generic code. If a user's routine requires only operations provided by the LinOp interface, the same code can be used for any kind of linear operators, independent of whether these are matrices, solvers or preconditioners. This feature is also extensively used in Ginkgo itself. For example, a preconditioner used inside a Krylov solver is a LinOp. This allows the user to supply a wide variety of preconditioners: either the ones which were designed to be used in this scenario (like ILU or block-Jacobi), a user-supplied matrix which is known to be a good preconditioner for the specific problem, or even another solver (e.g., if constructing a flexible GMRES solver).

For example, a matrix free implementation would require the user to provide an apply implementation and instead of passing the generated matrix to the solver, they would have to provide their apply implementation for all the executors needed and no other code needs to be changed. See The custom-matrix-format program example for more details.

Linear operator as a concept

The linear operator (LinOp) is a base class for all linear algebra objects in Ginkgo. The main benefit of having a single base class for the entire collection of linear algebra objects (as opposed to having separate hierarchies for matrices, solvers and preconditioners) is the generality it provides.

First, since all subclasses provide a common interface, the library users are exposed to a smaller set of routines. For example, a matrix-vector product, a preconditioner application, or even a system solve are just different terms given to the operation of applying a certain linear operator to a vector. As such, Ginkgo uses the same routine name, LinOp::apply() for each of these operations, where the actual operation performed depends on the type of linear operator involved in the operation.

Second, a common interface often allows for writing more generic code. If a user's routine requires only operations provided by the LinOp interface, the same code can be used for any kind of linear operators, independent of whether these are matrices, solvers or preconditioners. This feature is also extensively used in Ginkgo itself. For example, a preconditioner used inside a Krylov solver is a LinOp. This allows the user to supply a wide variety of preconditioners: either the ones which were designed to be used in this scenario (like ILU or block-Jacobi), a user-supplied matrix which is known to be a good preconditioner for the specific problem, or even another solver (e.g., if constructing a flexible GMRES solver).

A key observation for providing a unified interface for matrices, solvers, and preconditioners is that the most common operation performed on all of them can be expressed as an application of a linear operator to a vector:

the sparse matrix-vector product with a matrix is a linear operator application ;
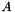the application of a preconditioner is a linear operator application 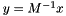$y = M^{-1}x$ , where 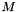is an approximation of the original system matrix 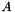(thus a preconditioner represents an "approximate inverse" operator $M^{-1}$ ).
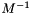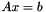the system solve can be viewed as linear operator application 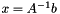$x = A^{-1}b$ (it goes without saying that the implementation of linear system solves does not follow this conceptual idea), so a linear system solver can be viewed as a representation of the operator $A^{-1}$ .

Finally, direct manipulation of LinOp objects is rarely required in simple scenarios. As an illustrative example, one could construct a fixed-point iteration routine 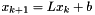$x_{k+1} = Lx_k + b$ as follows:

std::unique_ptr<matrix::Dense<>> calculate_fixed_point(
        int iters, const LinOp *L, const matrix::Dense<> *x0
        const matrix::Dense<> *b)
{
    auto x = gko::clone(x0);
    auto tmp = gko::clone(x0);
    auto one = Dense<>::create(L->get_executor(), {1.0,});
    for (int i = 0; i < iters; ++i) {
        L->apply(gko::lend(tmp), gko::lend(x));
        x->add_scaled(gko::lend(one), gko::lend(b));
        tmp->copy_from(gko::lend(x));
    }
    return x;
}

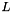Here, if $L$ is a matrix, LinOp::apply() refers to the matrix vector product, and L->apply(a, b) computes 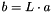$b = L \cdot a$ . x->add_scaled(one.get(), b.get()) is the axpy vector update 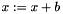$x:=x+b$ .

The interesting part of this example is the apply() routine at line 4 of the function body. Since this routine is part of the LinOp base class, the fixed-point iteration routine can calculate a fixed point not only for matrices, but for any type of linear operator.

Linear Operators

Macro Definition Documentation

◆ GKO_CREATE_FACTORY_PARAMETERS

#define GKO_CREATE_FACTORY_PARAMETERS	(	_parameters_name,
		_factory_name
	)

Value:

public:                                                                \
    class _factory_name;                                               \
    struct _parameters_name##_type                                     \
        : ::gko::enable_parameters_type<_parameters_name##_type,       \
                                        _factory_name>

This Macro will generate a new type containing the parameters for the factory _factory_name.

For more details, see GKO_ENABLE_LIN_OP_FACTORY(). It is required to use this macro before calling the macro GKO_ENABLE_LIN_OP_FACTORY(). It is also required to use the same names for all parameters between both macros.

Parameters

_parameters_name	name of the parameters member in the class
_factory_name	name of the generated factory type

◆ GKO_ENABLE_BUILD_METHOD

#define GKO_ENABLE_BUILD_METHOD ( _factory_name )

Value:

static auto build()->decltype(_factory_name::create())                   \
    {                                                                        \
        return _factory_name::create();                                      \
    }                                                                        \
    static_assert(true,                                                      \
                  "This assert is used to counter the false positive extra " \
                  "semi-colon warnings")

Defines a build method for the factory, simplifying its construction by removing the repetitive typing of factory's name.

Parameters

_factory_name the factory for which to define the method

◆ GKO_ENABLE_LIN_OP_FACTORY

#define GKO_ENABLE_LIN_OP_FACTORY	(	_lin_op,
		_parameters_name,
		_factory_name
	)

Value:

public:                                                                      \
    const _parameters_name##_type &get_##_parameters_name() const            \
    {                                                                        \
        return _parameters_name##_;                                          \
    }                                                                        \
                                                                             \
    class _factory_name                                                      \
        : public ::gko::EnableDefaultLinOpFactory<_factory_name, _lin_op,    \
                                                  _parameters_name##_type> { \
        friend class ::gko::EnablePolymorphicObject<_factory_name,           \
                                                    ::gko::LinOpFactory>;    \
        friend class ::gko::enable_parameters_type<_parameters_name##_type,  \
                                                   _factory_name>;           \
        using ::gko::EnableDefaultLinOpFactory<                              \
            _factory_name, _lin_op,                                          \
            _parameters_name##_type>::EnableDefaultLinOpFactory;             \
    };                                                                       \
    friend ::gko::EnableDefaultLinOpFactory<_factory_name, _lin_op,          \
                                            _parameters_name##_type>;        \
                                                                             \
                                                                             \
private:                                                                     \
    _parameters_name##_type _parameters_name##_;                             \
                                                                             \
public:                                                                      \
    static_assert(true,                                                      \
                  "This assert is used to counter the false positive extra " \
                  "semi-colon warnings")

This macro will generate a default implementation of a LinOpFactory for the LinOp subclass it is defined in.

It is required to first call the macro GKO_CREATE_FACTORY_PARAMETERS() before this one in order to instantiate the parameters type first.

The list of parameters for the factory should be defined in a code block after the macro definition, and should contain a list of GKO_FACTORY_PARAMETER declarations. The class should provide a constructor with signature _lin_op(const _factory_name *, std::shared_ptr<const LinOp>) which the factory will use a callback to construct the object.

A minimal example of a linear operator is the following:

{c++}
struct MyLinOp : public EnableLinOp<MyLinOp> {
    GKO_ENABLE_LIN_OP_FACTORY(MyLinOp, my_parameters, Factory) {
        // a factory parameter named "my_value", of type int and default
        // value of 5
        int GKO_FACTORY_PARAMETER(my_value, 5);
    };
    // constructor needed by EnableLinOp
    explicit MyLinOp(std::shared_ptr<const Executor> exec) {
        : EnableLinOp<MyLinOp>(exec) {}
    // constructor needed by the factory
    explicit MyLinOp(const Factory *factory,
                     std::shared_ptr<const LinOp> matrix)
        : EnableLinOp<MyLinOp>(factory->get_executor()), matrix->get_size()),
          // store factory's parameters locally
          my_parameters_{factory->get_parameters()},
    {
         int value = my_parameters_.my_value;
         // do something with value
    }

MyLinOp can then be created as follows:

{c++}
auto exec = gko::ReferenceExecutor::create();
// create a factory with default `my_value` parameter
auto fact = MyLinOp::build().on(exec);
// create a operator using the factory:
auto my_op = fact->generate(gko::matrix::Identity::create(exec, 2));
std::cout << my_op->get_my_parameters().my_value;  // prints 5
// create a factory with custom `my_value` parameter
auto fact = MyLinOp::build().with_my_value(0).on(exec);
// create a operator using the factory:
auto my_op = fact->generate(gko::matrix::Identity::create(exec, 2));
std::cout << my_op->get_my_parameters().my_value;  // prints 0

Note: It is possible to combine both the #GKO_CREATE_FACTORY_PARAMETER() macro with this one in a unique macro for class templates (not with regular classes). Splitting this into two distinct macros allows to use them in all contexts. See https://stackoverflow.com/q/50202718/9385966 for more details.

Parameters

_lin_op	concrete operator for which the factory is to be created [CRTP parameter]
_parameters_name	name of the parameters member in the class (its type is `<_parameters_name>_type`, the protected member's name is `<_parameters_name>_`, and the public getter's name is `get_<_parameters_name>()`)
_factory_name	name of the generated factory type

◆ GKO_FACTORY_PARAMETER

#define GKO_FACTORY_PARAMETER	(	_name,
		...
	)

Value:

mutable _name{__VA_ARGS__};                                              \
                                                                             \
    template <typename... Args>                                              \
    auto with_##_name(Args &&... _value)                                     \
        const->const ::gko::xstd::decay_t<decltype(*this)> &                 \
    {                                                                        \
        using type = decltype(this->_name);                                  \
        this->_name = type{std::forward<Args>(_value)...};                   \
        return *this;                                                        \
    }                                                                        \
    static_assert(true,                                                      \
                  "This assert is used to counter the false positive extra " \
                  "semi-colon warnings")

Creates a factory parameter in the factory parameters structure.

Parameters

_name	name of the parameter
<strong>VA_ARGS</strong>	default value of the parameter

See also: GKO_ENABLE_LIN_OP_FACTORY for more details, and usage example

Typedef Documentation

◆ EnableDefaultLinOpFactory

template<typename ConcreteFactory , typename ConcreteLinOp , typename ParametersType , typename PolymorphicBase = LinOpFactory>

using gko::EnableDefaultLinOpFactory = typedef EnableDefaultFactory<ConcreteFactory, ConcreteLinOp, ParametersType, PolymorphicBase>

This is an alias for the EnableDefaultFactory mixin, which correctly sets the template parameters to enable a subclass of LinOpFactory.

Template Parameters

ConcreteFactory	the concrete factory which is being implemented [CRTP parmeter]
ConcreteLinOp	the concrete LinOp type which this factory produces, needs to have a constructor which takes a const ConcreteFactory *, and an std::shared_ptr<const LinOp> as parameters.
ParametersType	a subclass of enable_parameters_type template which defines all of the parameters of the factory
PolymorphicBase	parent of ConcreteFactory in the polymorphic hierarchy, has to be a subclass of LinOpFactory

Modules

Classes

Macros

Typedefs

Detailed Description

Advantages of this approach and usage

Linear operator as a concept

Macro Definition Documentation

◆ GKO_CREATE_FACTORY_PARAMETERS

◆ GKO_ENABLE_BUILD_METHOD

◆ GKO_ENABLE_LIN_OP_FACTORY

◆ GKO_FACTORY_PARAMETER

Typedef Documentation

◆ EnableDefaultLinOpFactory