Linear operators which support permutation should implement the Permutable interface. More...

#include <ginkgo/core/base/lin_op.hpp>

Inheritance diagram for gko::Permutable< IndexType >:

Public Member Functions
virtual std::unique_ptr< LinOp >	permute (const array< IndexType > *permutation_indices) const
	Returns a LinOp representing the symmetric row and column permutation of the Permutable object. More...

virtual std::unique_ptr< LinOp >	inverse_permute (const array< IndexType > *permutation_indices) const
	Returns a LinOp representing the symmetric inverse row and column permutation of the Permutable object. More...

virtual std::unique_ptr< LinOp >	row_permute (const array< IndexType > *permutation_indices) const =0
	Returns a LinOp representing the row permutation of the Permutable object. More...

virtual std::unique_ptr< LinOp >	column_permute (const array< IndexType > *permutation_indices) const =0
	Returns a LinOp representing the column permutation of the Permutable object. More...

virtual std::unique_ptr< LinOp >	inverse_row_permute (const array< IndexType > *permutation_indices) const =0
	Returns a LinOp representing the row permutation of the inverse permuted object. More...

virtual std::unique_ptr< LinOp >	inverse_column_permute (const array< IndexType > *permutation_indices) const =0
	Returns a LinOp representing the row permutation of the inverse permuted object. More...

Detailed Description

template<typename IndexType>
class gko::Permutable< IndexType >

Linear operators which support permutation should implement the Permutable interface.

It provides functions to permute the rows and columns of a LinOp, independently or symmetrically, and with a regular or inverted permutation.

After a regular row permutation with permutation array perm the row i in the output LinOp contains the row perm[i] from the input LinOp. After an inverse row permutation, the row perm[i] in the output LinOp contains the row i from the input LinOp. Equivalently, after a column permutation, the output stores in column i the column perm[i] from the input, and an inverse column permutation stores in column perm[i] the column i from the input. A symmetric permutation is functionally equivalent to calling as<Permutable>(A->row_permute(perm))->column_permute(perm), but the implementation can provide better performance due to kernel fusion.

Example: Permuting a Csr matrix:

 {c++}
//Permuting an object of LinOp type.
//The object you want to permute.
auto op = matrix::Csr::create(exec);
//Permute the object by first converting it to a Permutable type.
auto perm = op->row_permute(permutation_indices);

Member Function Documentation

◆ column_permute()

template<typename IndexType>

virtual std::unique_ptr<LinOp> gko::Permutable< IndexType >::column_permute ( const array< IndexType > * permutation_indices ) const

pure virtual

Returns a LinOp representing the column permutation of the Permutable object.

In the resulting LinOp, the column i contains the input column perm[i].

From the linear algebra perspective, with 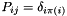$P_{ij} = \delta_{i \pi(i)}$ , this represents the operation $A P^T$ .

Parameters

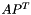permutation_indices the array of indices containing the permutation order perm.

Returns: a pointer to the new column permuted object

Implemented in gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, and gko::matrix::Csr< ValueType, IndexType >.

◆ inverse_column_permute()

template<typename IndexType>

virtual std::unique_ptr<LinOp> gko::Permutable< IndexType >::inverse_column_permute ( const array< IndexType > * permutation_indices ) const

pure virtual

Returns a LinOp representing the row permutation of the inverse permuted object.

In the resulting LinOp, the column perm[i] contains the input column i.

From the linear algebra perspective, with 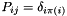$P_{ij} = \delta_{i \pi(i)}$ , this represents the operation $A P^{-T}$ .

Parameters

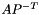permutation_indices the array of indices containing the permutation order perm.

Returns: a pointer to the new inverse permuted object

Implemented in gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, and gko::matrix::Csr< ValueType, IndexType >.

◆ inverse_permute()

template<typename IndexType>

virtual std::unique_ptr<LinOp> gko::Permutable< IndexType >::inverse_permute ( const array< IndexType > * permutation_indices ) const

inlinevirtual

Returns a LinOp representing the symmetric inverse row and column permutation of the Permutable object.

In the resulting LinOp, the entry at location (perm[i],perm[j]) contains the input value (i,j).

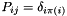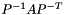From the linear algebra perspective, with $P_{ij} = \delta_{i \pi(i)}$ , this represents the operation $P^{-1} A P^{-T}$ .

Parameters

permutation_indices the array of indices containing the permutation order.

Returns: a pointer to the new permuted object

Reimplemented in gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, and gko::matrix::Csr< ValueType, IndexType >.

◆ inverse_row_permute()

template<typename IndexType>

virtual std::unique_ptr<LinOp> gko::Permutable< IndexType >::inverse_row_permute ( const array< IndexType > * permutation_indices ) const

pure virtual

Returns a LinOp representing the row permutation of the inverse permuted object.

In the resulting LinOp, the row perm[i] contains the input row i.

From the linear algebra perspective, with 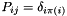$P_{ij} = \delta_{i \pi(i)}$ , this represents the operation $P^{-1} A$ .

Parameters

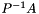permutation_indices the array of indices containing the permutation order perm.

Returns: a pointer to the new inverse permuted object

Implemented in gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, and gko::matrix::Csr< ValueType, IndexType >.

◆ permute()

template<typename IndexType>

virtual std::unique_ptr<LinOp> gko::Permutable< IndexType >::permute ( const array< IndexType > * permutation_indices ) const

inlinevirtual

Returns a LinOp representing the symmetric row and column permutation of the Permutable object.

In the resulting LinOp, the entry at location (i,j) contains the input value (perm[i],perm[j]).

From the linear algebra perspective, with 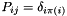$P_{ij} = \delta_{i \pi(i)}$ , this represents the operation $P A P^T$ .

Parameters

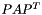permutation_indices the array of indices containing the permutation order.

Returns: a pointer to the new permuted object

Reimplemented in gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, and gko::matrix::Csr< ValueType, IndexType >.

◆ row_permute()

template<typename IndexType>

virtual std::unique_ptr<LinOp> gko::Permutable< IndexType >::row_permute ( const array< IndexType > * permutation_indices ) const

pure virtual

Returns a LinOp representing the row permutation of the Permutable object.

In the resulting LinOp, the row i contains the input row perm[i].

From the linear algebra perspective, with 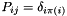$P_{ij} = \delta_{i \pi(i)}$ , this represents the operation $P A$ .

Parameters

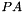permutation_indices the array of indices containing the permutation order.

Returns: a pointer to the new permuted object

Implemented in gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, gko::matrix::Dense< ValueType >, gko::matrix::Dense< value_type >, and gko::matrix::Csr< ValueType, IndexType >.

The documentation for this class was generated from the following file:

ginkgo/core/base/lin_op.hpp

Public Member Functions

Detailed Description

template<typename IndexType> class gko::Permutable< IndexType >

Example: Permuting a Csr matrix:

Member Function Documentation

◆ column_permute()

◆ inverse_column_permute()

◆ inverse_permute()

◆ inverse_row_permute()

◆ permute()

◆ row_permute()

template<typename IndexType>
class gko::Permutable< IndexType >