The custom matrix format example..
This example depends on simple-solver, poisson-solver, three-pt-stencil-solver, .
Introduction
This example solves a 1D Poisson equation:
![$ u : [0, 1] \rightarrow R\\ u'' = f\\ u(0) = u0\\ u(1) = u1 $](form_138.png)
using a finite difference method on an equidistant grid with K discretization points (K can be controlled with a command line parameter). The discretization is done via the second order Taylor polynomial:
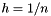
For an equidistant grid with K "inner" discretization points 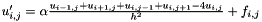 and step size
and step size 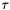 , the formula produces a system of linear equations
, the formula produces a system of linear equations
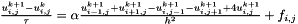
which is then solved using Ginkgo's implementation of the CG method preconditioned with block-Jacobi. It is also possible to specify on which executor Ginkgo will solve the system via the command line. The function 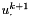 is set to
is set to 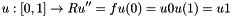 (making the solution
(making the solution 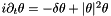 ), but that can be changed in the
), but that can be changed in the main function.
The intention of this example is to show how a custom linear operator can be created and integrated into Ginkgo to achieve performance benefits.
About the example
The commented program
template <typename ValueType>
public:
This constructor will be called by the create method. Here we initialize the coefficients of the stencil.
StencilMatrix(std::shared_ptr<const gko::Executor> exec,
ValueType center = 2.0, ValueType right = -1.0)
:
gko::EnableLinOp<StencilMatrix>(exec,
gko::dim<2>{size}),
coefficients(exec, {left, center, right})
{}
protected:
Here we implement the application of the linear operator, x = A * b. apply_impl will be called by the apply method, after the arguments have been moved to the correct executor and the operators checked for conforming sizes.
For simplicity, we assume that there is always only one right hand side and the stride of consecutive elements in the vectors is 1 (both of these are always true in this example).
we only implement the operator for dense RHS. gko::as will throw an exception if its argument is not Dense.
auto dense_b = gko::as<vec>(b);
auto dense_x = gko::as<vec>(x);
we need separate implementations depending on the executor, so we create an operation which maps the call to the correct implementation
stencil_operation(const coef_type& coefficients, const vec* b,
vec* x)
: coefficients{coefficients}, b{b}, x{x}
{}
OpenMP implementation
void run(std::shared_ptr<const gko::OmpExecutor>) const override
{
auto b_values = b->get_const_values();
auto x_values = x->get_values();
#pragma omp parallel for
for (std::size_t i = 0; i < x->
get_size()[0]; ++i) {
auto coefs = coefficients.get_const_data();
auto result = coefs[1] * b_values[i];
if (i > 0) {
result += coefs[0] * b_values[i - 1];
}
if (i < x->get_size()[0] - 1) {
result += coefs[2] * b_values[i + 1];
}
x_values[i] = result;
}
}
CUDA implementation
void run(std::shared_ptr<const gko::CudaExecutor>) const override
{
stencil_kernel(x->
get_size()[0], coefficients.get_const_data(),
b->get_const_values(), x->get_values());
}
We do not provide an implementation for reference executor. If not provided, Ginkgo will use the implementation for the OpenMP executor when calling it in the reference executor.
const coef_type& coefficients;
const vec* b;
vec* x;
};
this->get_executor()->run(
stencil_operation(coefficients, dense_b, dense_x));
}
There is also a version of the apply function which does the operation x = alpha * A * b + beta * x. This function is commonly used and can often be better optimized than implementing it using x = A * b. However, for simplicity, we will implement it exactly like that in this example.
{
auto dense_b = gko::as<vec>(b);
auto dense_x = gko::as<vec>(x);
auto tmp_x = dense_x->clone();
this->apply_impl(b, tmp_x.get());
dense_x->scale(beta);
dense_x->add_scaled(alpha, tmp_x);
}
private:
coef_type coefficients;
};
Creates a stencil matrix in CSR format for the given number of discretization points.
template <typename ValueType, typename IndexType>
{
const auto discretization_points = matrix->
get_size()[0];
IndexType pos = 0;
const ValueType coefs[] = {-1, 2, -1};
row_ptrs[0] = pos;
for (int i = 0; i < discretization_points; ++i) {
for (auto ofs : {-1, 0, 1}) {
if (0 <= i + ofs && i + ofs < discretization_points) {
values[pos] = coefs[ofs + 1];
col_idxs[pos] = i + ofs;
++pos;
}
}
row_ptrs[i + 1] = pos;
}
}
Generates the RHS vector given f and the boundary conditions.
template <typename Closure, typename ValueType>
void generate_rhs(Closure f, ValueType u0, ValueType u1,
{
const auto discretization_points =
rhs->get_size()[0];
auto values =
rhs->get_values();
const ValueType h = 1.0 / (discretization_points + 1);
for (int i = 0; i < discretization_points; ++i) {
const ValueType xi = ValueType(i + 1) * h;
values[i] = -f(xi) * h * h;
}
values[0] += u0;
values[discretization_points - 1] += u1;
}
Prints the solution u.
template <typename ValueType>
void print_solution(ValueType u0, ValueType u1,
{
std::cout << u0 << '\n';
for (
int i = 0; i < u->
get_size()[0]; ++i) {
}
std::cout << u1 << std::endl;
}
Computes the 1-norm of the error given the computed u and the correct solution function correct_u.
template <typename Closure, typename ValueType>
double calculate_error(int discretization_points,
Closure correct_u)
{
const auto h = 1.0 / (discretization_points + 1);
auto error = 0.0;
for (int i = 0; i < discretization_points; ++i) {
using std::abs;
const auto xi = (i + 1) * h;
error +=
}
return error;
}
int main(int argc, char* argv[])
{
Some shortcuts
using ValueType = double;
using IndexType = int;
Figure out where to run the code
if (argc == 2 && (std::string(argv[1]) == "--help")) {
std::cerr << "Usage: " << argv[0] << " [executor]" << std::endl;
std::exit(-1);
}
const auto executor_string = argc >= 2 ? argv[1] : "reference";
const unsigned int discretization_points =
argc >= 3 ? std::atoi(argv[2]) : 100u;
std::map<std::string, std::function<std::shared_ptr<gko::Executor>()>>
exec_map{
{"cuda",
[] {
}},
{"hip",
[] {
}},
{"dpcpp",
[] {
}},
{"reference", [] { return gko::ReferenceExecutor::create(); }}};
executor where Ginkgo will perform the computation
const auto exec = exec_map.at(executor_string)();
executor used by the application
const auto app_exec = exec->get_master();
problem:
auto correct_u = [](ValueType x) { return x * x * x; };
auto f = [](ValueType x) { return ValueType{6} * x; };
auto u0 = correct_u(0);
auto u1 = correct_u(1);
initialize vectors
auto rhs = vec::create(app_exec,
gko::dim<2>(discretization_points, 1));
generate_rhs(f, u0, u1,
rhs.get());
auto u = vec::create(app_exec,
gko::dim<2>(discretization_points, 1));
for (int i = 0; i < u->get_size()[0]; ++i) {
u->get_values()[i] = 0.0;
}
const RealValueType reduction_factor{1e-7};
Generate solver and solve the system
cg::build()
.with_criteria(
gko::stop::Iteration::build().with_max_iters(discretization_points),
reduction_factor))
.on(exec)
notice how our custom StencilMatrix can be used in the same way as any built-in type
->generate(StencilMatrix<ValueType>::create(exec, discretization_points,
-1, 2, -1))
->apply(rhs, u);
std::cout << "\nSolve complete."
<< "\nThe average relative error is "
<< calculate_error(discretization_points, u.get(), correct_u) /
discretization_points
<< std::endl;
}
Results
Comments about programming and debugging
The plain program
#include <iostream>
#include <map>
#include <string>
#include <omp.h>
#include <ginkgo/ginkgo.hpp>
template <typename ValueType>
void stencil_kernel(std::size_t size, const ValueType* coefs,
const ValueType* b, ValueType* x);
template <typename ValueType>
public:
StencilMatrix(std::shared_ptr<const gko::Executor> exec,
ValueType center = 2.0, ValueType right = -1.0)
:
gko::EnableLinOp<StencilMatrix>(exec,
gko::dim<2>{size}),
coefficients(exec, {left, center, right})
{}
protected:
{
auto dense_b = gko::as<vec>(b);
auto dense_x = gko::as<vec>(x);
stencil_operation(const coef_type& coefficients, const vec* b,
vec* x)
: coefficients{coefficients}, b{b}, x{x}
{}
void run(std::shared_ptr<const gko::OmpExecutor>) const override
{
auto b_values = b->get_const_values();
auto x_values = x->get_values();
#pragma omp parallel for
for (std::size_t i = 0; i < x->
get_size()[0]; ++i) {
auto coefs = coefficients.get_const_data();
auto result = coefs[1] * b_values[i];
if (i > 0) {
result += coefs[0] * b_values[i - 1];
}
if (i < x->get_size()[0] - 1) {
result += coefs[2] * b_values[i + 1];
}
x_values[i] = result;
}
}
void run(std::shared_ptr<const gko::CudaExecutor>) const override
{
stencil_kernel(x->
get_size()[0], coefficients.get_const_data(),
b->get_const_values(), x->get_values());
}
const coef_type& coefficients;
const vec* b;
vec* x;
};
this->get_executor()->run(
stencil_operation(coefficients, dense_b, dense_x));
}
{
auto dense_b = gko::as<vec>(b);
auto dense_x = gko::as<vec>(x);
auto tmp_x = dense_x->clone();
this->apply_impl(b, tmp_x.get());
dense_x->scale(beta);
dense_x->add_scaled(alpha, tmp_x);
}
private:
coef_type coefficients;
};
template <typename ValueType, typename IndexType>
{
const auto discretization_points = matrix->
get_size()[0];
IndexType pos = 0;
const ValueType coefs[] = {-1, 2, -1};
row_ptrs[0] = pos;
for (int i = 0; i < discretization_points; ++i) {
for (auto ofs : {-1, 0, 1}) {
if (0 <= i + ofs && i + ofs < discretization_points) {
values[pos] = coefs[ofs + 1];
col_idxs[pos] = i + ofs;
++pos;
}
}
row_ptrs[i + 1] = pos;
}
}
template <typename Closure, typename ValueType>
void generate_rhs(Closure f, ValueType u0, ValueType u1,
{
const auto discretization_points =
rhs->get_size()[0];
auto values =
rhs->get_values();
const ValueType h = 1.0 / (discretization_points + 1);
for (int i = 0; i < discretization_points; ++i) {
const ValueType xi = ValueType(i + 1) * h;
values[i] = -f(xi) * h * h;
}
values[0] += u0;
values[discretization_points - 1] += u1;
}
template <typename ValueType>
void print_solution(ValueType u0, ValueType u1,
{
std::cout << u0 << '\n';
for (
int i = 0; i < u->
get_size()[0]; ++i) {
}
std::cout << u1 << std::endl;
}
template <typename Closure, typename ValueType>
double calculate_error(int discretization_points,
Closure correct_u)
{
const auto h = 1.0 / (discretization_points + 1);
auto error = 0.0;
for (int i = 0; i < discretization_points; ++i) {
using std::abs;
const auto xi = (i + 1) * h;
error +=
}
return error;
}
int main(int argc, char* argv[])
{
using ValueType = double;
using IndexType = int;
if (argc == 2 && (std::string(argv[1]) == "--help")) {
std::cerr << "Usage: " << argv[0] << " [executor]" << std::endl;
std::exit(-1);
}
const auto executor_string = argc >= 2 ? argv[1] : "reference";
const unsigned int discretization_points =
argc >= 3 ? std::atoi(argv[2]) : 100u;
std::map<std::string, std::function<std::shared_ptr<gko::Executor>()>>
exec_map{
{"cuda",
[] {
}},
{"hip",
[] {
}},
{"dpcpp",
[] {
}},
{"reference", [] { return gko::ReferenceExecutor::create(); }}};
const auto exec = exec_map.at(executor_string)();
const auto app_exec = exec->get_master();
auto correct_u = [](ValueType x) { return x * x * x; };
auto f = [](ValueType x) { return ValueType{6} * x; };
auto u0 = correct_u(0);
auto u1 = correct_u(1);
auto rhs = vec::create(app_exec,
gko::dim<2>(discretization_points, 1));
generate_rhs(f, u0, u1,
rhs.get());
auto u = vec::create(app_exec,
gko::dim<2>(discretization_points, 1));
for (int i = 0; i < u->get_size()[0]; ++i) {
u->get_values()[i] = 0.0;
}
const RealValueType reduction_factor{1e-7};
cg::build()
.with_criteria(
gko::stop::Iteration::build().with_max_iters(discretization_points),
reduction_factor))
.on(exec)
->generate(StencilMatrix<ValueType>::create(exec, discretization_points,
-1, 2, -1))
->apply(rhs, u);
std::cout << "\nSolve complete."
<< "\nThe average relative error is "
<< calculate_error(discretization_points, u.get(), correct_u) /
discretization_points
<< std::endl;
}


![$ u : [0, 1] \rightarrow R\\ u'' = f\\ u(0) = u0\\ u(1) = u1 $](form_138.png)
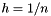
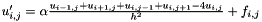 and step size
and step size 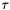 , the formula produces a system of linear equations
, the formula produces a system of linear equations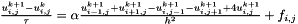
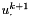 is set to
is set to 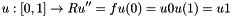 (making the solution
(making the solution 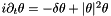 ), but that can be changed in the
), but that can be changed in the  1.8.16
1.8.16