The heat equation example..
This example depends on simple-solver, three-pt-stencil-solver.
Introduction
This example solves a 2D heat conduction equation
![$ u : [0, d]^2 \rightarrow R\\ \partial_t u = \delta u + f $](form_146.png)
with Dirichlet boundary conditions and given initial condition and constant-in-time source function f.
The partial differential equation (PDE) is solved with a finite difference spatial discretization on an equidistant grid: For n grid points, and grid distance 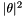 we write
we write
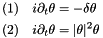
We then build an implicit Euler integrator by discretizing with time step 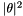
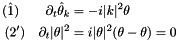
and solve the resulting linear system for 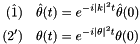 using Ginkgo's CG solver preconditioned with an incomplete Cholesky factorization for each time step, occasionally writing the resulting grid values into a video file using OpenCV and a custom color mapping.
using Ginkgo's CG solver preconditioned with an incomplete Cholesky factorization for each time step, occasionally writing the resulting grid values into a video file using OpenCV and a custom color mapping.
The intention of this example is to provide a mini-app showing matrix assembly, vector initialization, solver setup and the use of Ginkgo in a more complex setting.
About the example
The commented program
The intention of this example is to provide a mini-app showing matrix assembly,
vector initialization,
solver setup and the use of Ginkgo in a more complex
setting.
*****************************<DESCRIPTION>********************************** /
#include <chrono>
#include <fstream>
#include <iostream>
#include <opencv2/core.hpp>
#include <opencv2/videoio.hpp>
#include <ginkgo/ginkgo.hpp>
This function implements a simple Ginkgo-themed clamped color mapping for values in the range [0,5].
void set_val(unsigned char* data, double value)
{
RGB values for the 6 colors used for values 0, 1, ..., 5 We will interpolate linearly between these values.
double col_r[] = {255, 221, 129, 201, 249, 255};
double col_g[] = {255, 220, 130, 161, 158, 204};
double col_b[] = {255, 220, 133, 93, 24, 8};
value = std::max(0.0, value);
auto i = std::max(0, std::min(4, int(value)));
auto d = std::max(0.0, std::min(1.0, value - i));
OpenCV uses BGR instead of RGB by default, revert indices
data[2] = static_cast<unsigned char>(col_r[i + 1] * d + col_r[i] * (1 - d));
data[1] = static_cast<unsigned char>(col_g[i + 1] * d + col_g[i] * (1 - d));
data[0] = static_cast<unsigned char>(col_b[i + 1] * d + col_b[i] * (1 - d));
}
Initialize video output with given dimension and FPS (frames per seconds)
std::pair<cv::VideoWriter, cv::Mat> build_output(int n, double fps)
{
cv::Size videosize{n, n};
auto output =
std::make_pair(cv::VideoWriter{}, cv::Mat{videosize, CV_8UC3});
auto fourcc = cv::VideoWriter::fourcc('a', 'v', 'c', '1');
output.first.open("heat.mp4", fourcc, fps, videosize);
return output;
}
Write the current frame to video output using the above color mapping
void output_timestep(std::pair<cv::VideoWriter, cv::Mat>& output, int n,
const double* data)
{
for (int i = 0; i < n; i++) {
auto row = output.second.ptr(i);
for (int j = 0; j < n; j++) {
set_val(&row[3 * j], data[i * n + j]);
}
}
output.first.write(output.second);
}
int main(int argc, char* argv[])
{
Problem parameters: simulation length
diffusion factor
scaling factor for heat source
Simulation parameters: inner grid points per discretization direction
number of simulation steps per second
auto steps_per_sec = 500;
number of video frames per second
number of grid points
grid point distance (ignoring boundary points)
auto h = 1.0 / (n + 1);
auto h2 = h * h;
time step size for the simulation
auto tau = 1.0 / steps_per_sec;
create a CUDA executor with an associated OpenMP host executor
load heat source and initial state vectors
std::ifstream initial_stream("data/gko_logo_2d.mtx");
std::ifstream source_stream("data/gko_text_2d.mtx");
auto source = gko::read<vec>(source_stream, exec);
auto in_vector = gko::read<vec>(initial_stream, exec);
create output vector with initial guess for
auto out_vector = in_vector->clone();
create scalar for source update
auto tau_source_scalar = gko::initialize<vec>({source_scale * tau}, exec);
create stencil matrix as shared_ptr for solver
auto stencil_matrix =
gko::share(mtx::create(exec));
assemble matrix
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
auto c = i * n + j;
auto c_val = diffusion * tau * 4.0 / h2 + 1.0;
auto off_val = -diffusion * tau / h2;
for each grid point: insert 5 stencil points with Dirichlet boundary conditions, i.e. with zero boundary value
if (i > 0) {
mtx_data.nonzeros.emplace_back(c, c - n, off_val);
}
if (j > 0) {
mtx_data.nonzeros.emplace_back(c, c - 1, off_val);
}
mtx_data.nonzeros.emplace_back(c, c, c_val);
if (j < n - 1) {
mtx_data.nonzeros.emplace_back(c, c + 1, off_val);
}
if (i < n - 1) {
mtx_data.nonzeros.emplace_back(c, c + n, off_val);
}
}
}
stencil_matrix->read(mtx_data);
prepare video output
auto output = build_output(n, fps);
build CG solver on stencil with incomplete Cholesky preconditioner stopping at 1e-10 relative accuracy
.with_baseline(gko::stop::mode::rhs_norm)
.with_reduction_factor(1e-10))
.on(exec)
->generate(stencil_matrix);
time stamp of the last output frame (initialized to a sentinel value)
execute implicit Euler method: for each timestep, solve stencil system
for (double t = 0; t < t0; t += tau) {
if enough time has passed, output the next video frame
if (t - last_t > 1.0 / fps) {
last_t = t;
std::cout << t << std::endl;
output_timestep(
output, n,
->get_const_values());
}
add heat source contribution
in_vector->add_scaled(tau_source_scalar, source);
execute Euler step
solver->apply(in_vector, out_vector);
swap input and output
std::swap(in_vector, out_vector);
}
}
Results
The program will generate a video file named heat.mp4 and output the timestamp of each generated frame.
Comments about programming and debugging
The plain program
#include <chrono>
#include <fstream>
#include <iostream>
#include <opencv2/core.hpp>
#include <opencv2/videoio.hpp>
#include <ginkgo/ginkgo.hpp>
void set_val(unsigned char* data, double value)
{
double col_r[] = {255, 221, 129, 201, 249, 255};
double col_g[] = {255, 220, 130, 161, 158, 204};
double col_b[] = {255, 220, 133, 93, 24, 8};
value = std::max(0.0, value);
auto i = std::max(0, std::min(4, int(value)));
auto d = std::max(0.0, std::min(1.0, value - i));
data[2] = static_cast<unsigned char>(col_r[i + 1] * d + col_r[i] * (1 - d));
data[1] = static_cast<unsigned char>(col_g[i + 1] * d + col_g[i] * (1 - d));
data[0] = static_cast<unsigned char>(col_b[i + 1] * d + col_b[i] * (1 - d));
}
std::pair<cv::VideoWriter, cv::Mat> build_output(int n, double fps)
{
cv::Size videosize{n, n};
auto output =
std::make_pair(cv::VideoWriter{}, cv::Mat{videosize, CV_8UC3});
auto fourcc = cv::VideoWriter::fourcc('a', 'v', 'c', '1');
output.first.open("heat.mp4", fourcc, fps, videosize);
return output;
}
void output_timestep(std::pair<cv::VideoWriter, cv::Mat>& output, int n,
const double* data)
{
for (int i = 0; i < n; i++) {
auto row = output.second.ptr(i);
for (int j = 0; j < n; j++) {
set_val(&row[3 * j], data[i * n + j]);
}
}
output.first.write(output.second);
}
int main(int argc, char* argv[])
{
auto t0 = 5.0;
auto diffusion = 0.0005;
auto source_scale = 2.5;
auto n = 256;
auto steps_per_sec = 500;
auto fps = 25;
auto n2 = n * n;
auto h = 1.0 / (n + 1);
auto h2 = h * h;
auto tau = 1.0 / steps_per_sec;
std::ifstream initial_stream("data/gko_logo_2d.mtx");
std::ifstream source_stream("data/gko_text_2d.mtx");
auto source = gko::read<vec>(source_stream, exec);
auto in_vector = gko::read<vec>(initial_stream, exec);
auto out_vector = in_vector->clone();
auto tau_source_scalar = gko::initialize<vec>({source_scale * tau}, exec);
auto stencil_matrix =
gko::share(mtx::create(exec));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
auto c = i * n + j;
auto c_val = diffusion * tau * 4.0 / h2 + 1.0;
auto off_val = -diffusion * tau / h2;
if (i > 0) {
mtx_data.nonzeros.emplace_back(c, c - n, off_val);
}
if (j > 0) {
mtx_data.nonzeros.emplace_back(c, c - 1, off_val);
}
mtx_data.nonzeros.emplace_back(c, c, c_val);
if (j < n - 1) {
mtx_data.nonzeros.emplace_back(c, c + 1, off_val);
}
if (i < n - 1) {
mtx_data.nonzeros.emplace_back(c, c + n, off_val);
}
}
}
stencil_matrix->read(mtx_data);
auto output = build_output(n, fps);
.with_baseline(gko::stop::mode::rhs_norm)
.with_reduction_factor(1e-10))
.on(exec)
->generate(stencil_matrix);
double last_t = -t0;
for (double t = 0; t < t0; t += tau) {
if (t - last_t > 1.0 / fps) {
last_t = t;
std::cout << t << std::endl;
output_timestep(
output, n,
->get_const_values());
}
in_vector->add_scaled(tau_source_scalar, source);
solver->apply(in_vector, out_vector);
std::swap(in_vector, out_vector);
}
}


![$ u : [0, d]^2 \rightarrow R\\ \partial_t u = \delta u + f $](form_146.png)
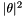 we write
we write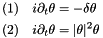
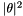
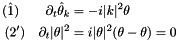
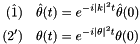 using Ginkgo's CG solver preconditioned with an incomplete Cholesky factorization for each time step, occasionally writing the resulting grid values into a video file using OpenCV and a custom color mapping.
using Ginkgo's CG solver preconditioned with an incomplete Cholesky factorization for each time step, occasionally writing the resulting grid values into a video file using OpenCV and a custom color mapping. 1.8.16
1.8.16