The 3-point stencil example..
This example depends on simple-solver, poisson-solver.
Introduction
This example solves a 1D Poisson equation:
![$ u : [0, 1] \rightarrow R\\ u'' = f\\ u(0) = u0\\ u(1) = u1 $](form_124.png)
using a finite difference method on an equidistant grid with K discretization points (K can be controlled with a command line parameter). The discretization is done via the second order Taylor polynomial:
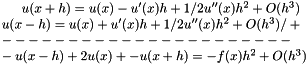
For an equidistant grid with K "inner" discretization points 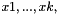 and step size
and step size 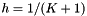 , the formula produces a system of linear equations
, the formula produces a system of linear equations
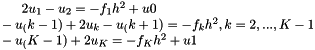
which is then solved using Ginkgo's implementation of the CG method preconditioned with block-Jacobi. It is also possible to specify on which executor Ginkgo will solve the system via the command line. The function 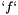 is set to
is set to 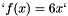 (making the solution
(making the solution 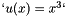 ), but that can be changed in the
), but that can be changed in the main function.
The intention of the example is to show how Ginkgo can be integrated into existing software - the generate_stencil_matrix, generate_rhs, print_solution, compute_error and main function do not reference Ginkgo at all (i.e. they could have been there before the application developer decided to use Ginkgo, and the only part where Ginkgo is introduced is inside the solve_system function.
About the example
The commented program
The function `f` is set to `f(x) = 6x` (making the solution `u(x) = x^3`), but
that can be changed in the `main` function.
The intention of the example is to show how Ginkgo can be integrated into
existing software - the `generate_stencil_matrix`, `generate_rhs`,
`print_solution`, `compute_error` and `main` function do not reference Ginkgo at
all (i.e. they could have been there before the application developer decided to
use Ginkgo, and the only part where Ginkgo is introduced is inside the
`solve_system` function.
*****************************<DESCRIPTION>********************************** /
#include <ginkgo/ginkgo.hpp>
#include <iostream>
#include <map>
#include <string>
#include <vector>
Creates a stencil matrix in CSR format for the given number of discretization points.
template <typename ValueType, typename IndexType>
void generate_stencil_matrix(IndexType discretization_points,
IndexType* row_ptrs, IndexType* col_idxs,
ValueType* values)
{
IndexType pos = 0;
const ValueType coefs[] = {-1, 2, -1};
row_ptrs[0] = pos;
for (IndexType i = 0; i < discretization_points; ++i) {
for (auto ofs : {-1, 0, 1}) {
if (0 <= i + ofs && i + ofs < discretization_points) {
values[pos] = coefs[ofs + 1];
col_idxs[pos] = i + ofs;
++pos;
}
}
row_ptrs[i + 1] = pos;
}
}
Generates the RHS vector given f and the boundary conditions.
template <typename Closure, typename ValueType, typename IndexType>
void generate_rhs(IndexType discretization_points, Closure f, ValueType u0,
ValueType u1, ValueType* rhs)
{
const ValueType h = 1.0 / (discretization_points + 1);
for (IndexType i = 0; i < discretization_points; ++i) {
const ValueType xi = ValueType(i + 1) * h;
}
rhs[discretization_points - 1] += u1;
}
Prints the solution u.
template <typename ValueType, typename IndexType>
void print_solution(IndexType discretization_points, ValueType u0, ValueType u1,
const ValueType* u)
{
std::cout << u0 << '\n';
for (IndexType i = 0; i < discretization_points; ++i) {
std::cout << u[i] << '\n';
}
std::cout << u1 << std::endl;
}
Computes the 1-norm of the error given the computed u and the correct solution function correct_u.
template <typename Closure, typename ValueType, typename IndexType>
const ValueType* u,
Closure correct_u)
{
const ValueType h = 1.0 / (discretization_points + 1);
for (IndexType i = 0; i < discretization_points; ++i) {
using std::abs;
const ValueType xi = ValueType(i + 1) * h;
error +=
abs(u[i] - correct_u(xi)) /
abs(correct_u(xi));
}
return error;
}
template <typename ValueType, typename IndexType>
void solve_system(const std::string& executor_string,
IndexType discretization_points, IndexType* row_ptrs,
IndexType* col_idxs, ValueType* values, ValueType* rhs,
{
Some shortcuts
const auto& dp = discretization_points;
Figure out where to run the code
std::map<std::string, std::function<std::shared_ptr<gko::Executor>()>>
exec_map{
{"cuda",
[] {
}},
{"hip",
[] {
}},
{"dpcpp",
[] {
}},
{"reference", [] { return gko::ReferenceExecutor::create(); }}};
executor where Ginkgo will perform the computation
const auto exec = exec_map.at(executor_string)();
executor where the application initialized the data
Tell Ginkgo to use the data in our application
Matrix: we have to set the executor of the matrix to the one where we want SpMVs to run (in this case exec). When creating array views, we have to specify the executor where the data is (in this case app_exec).
If the two do not match, Ginkgo will automatically create a copy of the data on exec (however, it will not copy the data back once it is done
- here this is not important since we are not modifying the matrix).
val_array::view(app_exec, 3 * dp - 2, values),
idx_array::view(app_exec, 3 * dp - 2, col_idxs),
idx_array::view(app_exec, dp + 1, row_ptrs));
RHS: similar to matrix
val_array::view(app_exec, dp, rhs), 1);
Solution: we have to be careful here - if the executors are different, once we compute the solution the array will not be automatically copied back to the original memory locations. Fortunately, whenever apply is called on a linear operator (e.g. matrix, solver) the arguments automatically get copied to the executor where the operator is, and copied back once the operation is completed. Thus, in this case, we can just define the solution on app_exec, and it will be automatically transferred to/from exec if needed.
val_array::view(app_exec, dp, u), 1);
Generate solver
auto solver_gen =
cg::build()
.with_criteria(gko::stop::Iteration::build().with_max_iters(
.with_reduction_factor(reduction_factor))
.with_preconditioner(bj::build())
.on(exec);
Solve system
}
int main(int argc, char* argv[])
{
using ValueType = double;
using IndexType = int;
Print version information
if (argc == 2 && std::string(argv[1]) == "--help") {
std::cerr << "Usage: " << argv[0]
<< " [executor] [DISCRETIZATION_POINTS]" << std::endl;
std::exit(-1);
}
const auto executor_string = argc >= 2 ? argv[1] : "reference";
const IndexType discretization_points =
argc >= 3 ? std::atoi(argv[2]) : 100;
problem:
auto correct_u = [](ValueType x) { return x * x * x; };
auto f = [](ValueType x) { return ValueType(6) * x; };
auto u0 = correct_u(0);
auto u1 = correct_u(1);
matrix
std::vector<IndexType> row_ptrs(discretization_points + 1);
std::vector<IndexType> col_idxs(3 * discretization_points - 2);
std::vector<ValueType> values(3 * discretization_points - 2);
right hand side
std::vector<ValueType>
rhs(discretization_points);
solution
std::vector<ValueType> u(discretization_points, 0.0);
generate_stencil_matrix(discretization_points, row_ptrs.data(),
col_idxs.data(), values.data());
looking for solution u = x^3: f = 6x, u(0) = 0, u(1) = 1
generate_rhs(discretization_points, f, u0, u1,
rhs.data());
solve_system(executor_string, discretization_points, row_ptrs.data(),
col_idxs.data(), values.data(),
rhs.data(), u.data(),
reduction_factor);
Uncomment to print the solution print_solution<ValueType, IndexType>(discretization_points, 0, 1, u.data());
std::cout << "The average relative error is "
<< calculate_error(discretization_points, u.data(), correct_u) /
discretization_points
<< std::endl;
}
Results
This is the expected output:
The average relative error is 2.52236e-11
Comments about programming and debugging
The plain program
#include <ginkgo/ginkgo.hpp>
#include <iostream>
#include <map>
#include <string>
#include <vector>
template <typename ValueType, typename IndexType>
void generate_stencil_matrix(IndexType discretization_points,
IndexType* row_ptrs, IndexType* col_idxs,
ValueType* values)
{
IndexType pos = 0;
const ValueType coefs[] = {-1, 2, -1};
row_ptrs[0] = pos;
for (IndexType i = 0; i < discretization_points; ++i) {
for (auto ofs : {-1, 0, 1}) {
if (0 <= i + ofs && i + ofs < discretization_points) {
values[pos] = coefs[ofs + 1];
col_idxs[pos] = i + ofs;
++pos;
}
}
row_ptrs[i + 1] = pos;
}
}
template <typename Closure, typename ValueType, typename IndexType>
void generate_rhs(IndexType discretization_points, Closure f, ValueType u0,
ValueType u1, ValueType* rhs)
{
const ValueType h = 1.0 / (discretization_points + 1);
for (IndexType i = 0; i < discretization_points; ++i) {
const ValueType xi = ValueType(i + 1) * h;
}
rhs[discretization_points - 1] += u1;
}
template <typename ValueType, typename IndexType>
void print_solution(IndexType discretization_points, ValueType u0, ValueType u1,
const ValueType* u)
{
std::cout << u0 << '\n';
for (IndexType i = 0; i < discretization_points; ++i) {
std::cout << u[i] << '\n';
}
std::cout << u1 << std::endl;
}
template <typename Closure, typename ValueType, typename IndexType>
const ValueType* u,
Closure correct_u)
{
const ValueType h = 1.0 / (discretization_points + 1);
for (IndexType i = 0; i < discretization_points; ++i) {
using std::abs;
const ValueType xi = ValueType(i + 1) * h;
error +=
abs(u[i] - correct_u(xi)) /
abs(correct_u(xi));
}
return error;
}
template <typename ValueType, typename IndexType>
void solve_system(const std::string& executor_string,
IndexType discretization_points, IndexType* row_ptrs,
IndexType* col_idxs, ValueType* values, ValueType* rhs,
{
const auto& dp = discretization_points;
std::map<std::string, std::function<std::shared_ptr<gko::Executor>()>>
exec_map{
{"cuda",
[] {
}},
{"hip",
[] {
}},
{"dpcpp",
[] {
}},
{"reference", [] { return gko::ReferenceExecutor::create(); }}};
const auto exec = exec_map.at(executor_string)();
val_array::view(app_exec, 3 * dp - 2, values),
idx_array::view(app_exec, 3 * dp - 2, col_idxs),
idx_array::view(app_exec, dp + 1, row_ptrs));
val_array::view(app_exec, dp, rhs), 1);
val_array::view(app_exec, dp, u), 1);
auto solver_gen =
cg::build()
.with_criteria(gko::stop::Iteration::build().with_max_iters(
.with_reduction_factor(reduction_factor))
.with_preconditioner(bj::build())
.on(exec);
}
int main(int argc, char* argv[])
{
using ValueType = double;
using IndexType = int;
if (argc == 2 && std::string(argv[1]) == "--help") {
std::cerr << "Usage: " << argv[0]
<< " [executor] [DISCRETIZATION_POINTS]" << std::endl;
std::exit(-1);
}
const auto executor_string = argc >= 2 ? argv[1] : "reference";
const IndexType discretization_points =
argc >= 3 ? std::atoi(argv[2]) : 100;
auto correct_u = [](ValueType x) { return x * x * x; };
auto f = [](ValueType x) { return ValueType(6) * x; };
auto u0 = correct_u(0);
auto u1 = correct_u(1);
std::vector<IndexType> row_ptrs(discretization_points + 1);
std::vector<IndexType> col_idxs(3 * discretization_points - 2);
std::vector<ValueType> values(3 * discretization_points - 2);
std::vector<ValueType>
rhs(discretization_points);
std::vector<ValueType> u(discretization_points, 0.0);
generate_stencil_matrix(discretization_points, row_ptrs.data(),
col_idxs.data(), values.data());
generate_rhs(discretization_points, f, u0, u1,
rhs.data());
solve_system(executor_string, discretization_points, row_ptrs.data(),
col_idxs.data(), values.data(),
rhs.data(), u.data(),
reduction_factor);
std::cout << "The average relative error is "
<< calculate_error(discretization_points, u.data(), correct_u) /
discretization_points
<< std::endl;
}


![$ u : [0, 1] \rightarrow R\\ u'' = f\\ u(0) = u0\\ u(1) = u1 $](form_124.png)
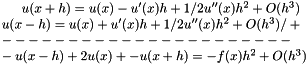
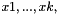 and step size
and step size 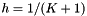 , the formula produces a system of linear equations
, the formula produces a system of linear equations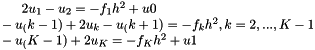
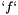 is set to
is set to 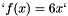 (making the solution
(making the solution 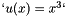 ), but that can be changed in the
), but that can be changed in the  1.8.16
1.8.16